Complete Coverage Path Planning

One of my primary responsibilities on UAV Forge last year was to design and implement our drone’s path planning algorithm. We were tasked with searching a region for targets in the most time-efficient manner possible.
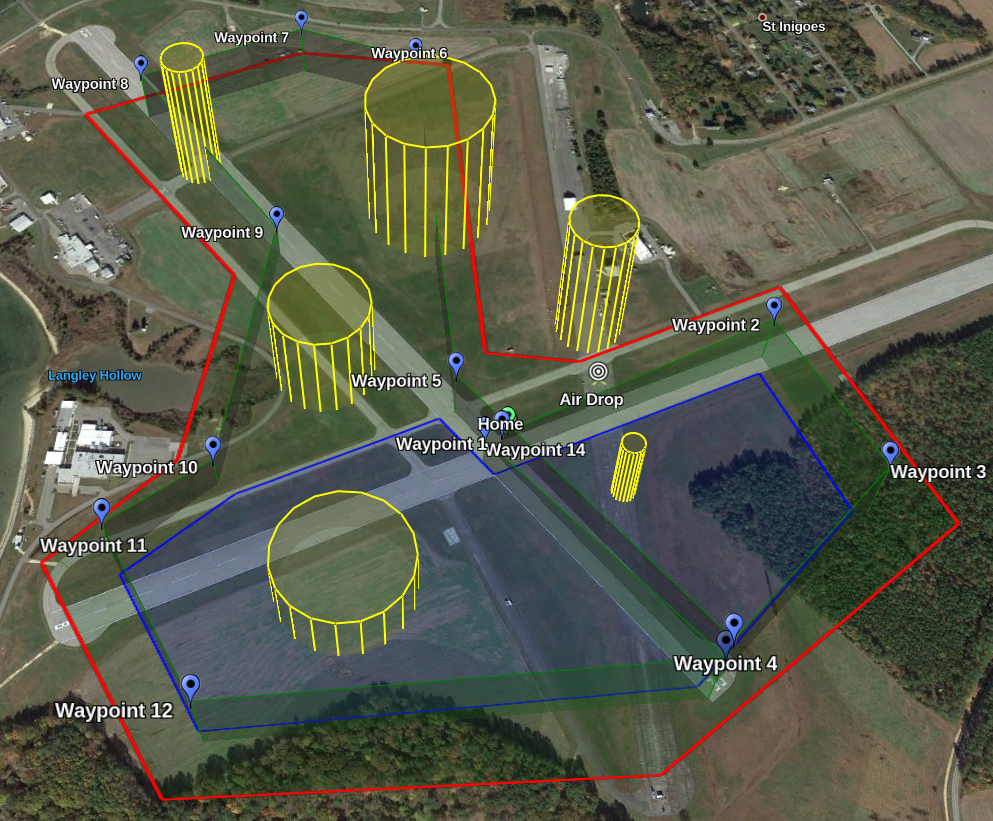
Since the competition does not provide the exact geographic location of each target, the drone must cover every point in the search area. The drone must complete this task while avoiding static obstacles and remaining inside the competition boundary. Below is a figure showing an example of a complete coverage path, similar to the one developed by our team.
Boustrophedon Decomposition
Our approach utilizes a method called boustrophedon cell decomposition, which first divides the search area into individual subregions. The path planning algorithm then sweeps each subregion individually. Boustrophedon decomposition is deterministic, meaning that we can guarantee completion of the algorithm within a finite time-frame.
Computing Convex and Concave Vertices
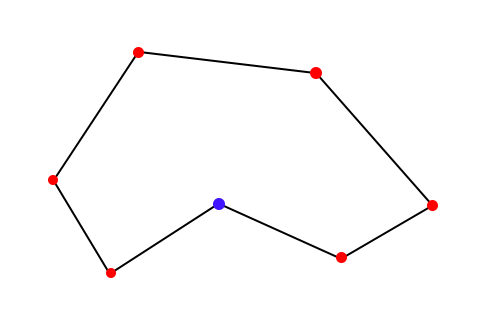
A key component to the development of the algorithm was the ability to easily identify concave and convex vertices of the boundary region. An example region is drawn below, with concave vertices labeled in blue and convex vertices labeled in red. Concave vertices denote a critical point in the geometry, and act as origin points for the lines that divide the boundary area into subregions.
The arrows in purple represent vectors that are collinear with lines that comprise the boundary. It is clear to see that the vectors make counterclockwise turns at convex vertices and clockwise turns at concave vertices. This can be represented mathematically by calculating the cross-product between the two vectors that intersect at any vertex. A positive cross-product result represents a convex vertex, and a negative cross-product result represents a concave vertex.
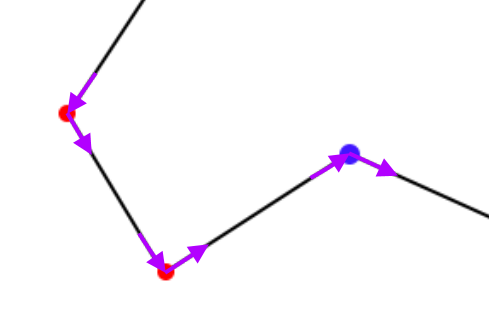
By iterating through every corner in the boundary using this strategy, it is trivial to identify every vertex as concave or convex.
Optimal Sweep Angle
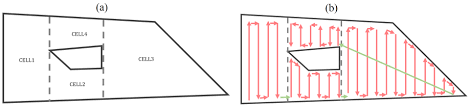
The first step in the boustrophedon decomposition algorithm is to divide the boundary into subregions. By drawing a line (purple) originating from each concave vertex in the region (blue), we can guarantee that each resulting subregion will be convex. The angle that our subregion dividing lines are drawn at is variable, and can result in vastly different subregion shapes.
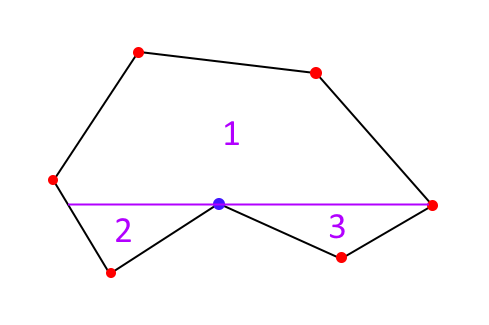
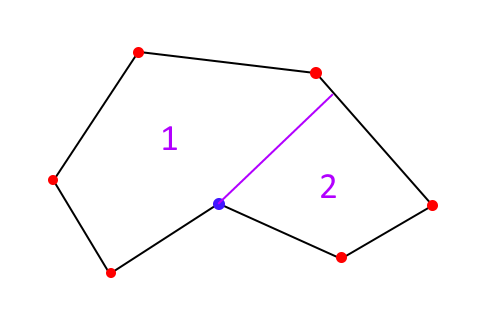
The figures above illustrate the difference in subregion shapes based on the sweep angle. In this case, a zero degree sweep angle results in three subregions, while a fourty-five degree sweep angle results in two subregions. Though the total area swept is equivalent in both cases, reducing the amount of subregions results in less time spent navigating between subregions.
Sweep angle can be iteratively optimized to fit different criteria such as number of subregions, length of total path, or size of subregions.
Sweeping Subregions
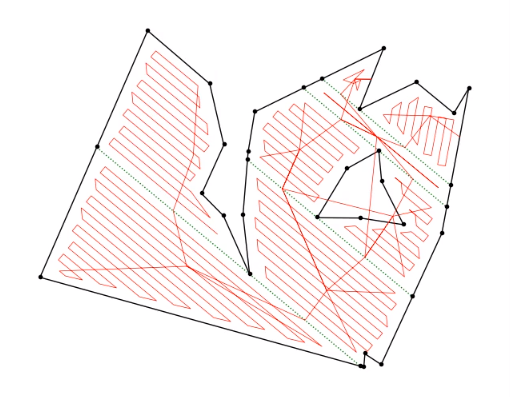
After the individual subregions are generated via drawing the sweep lines, they can be swept using a simple, back-and-forth pattern. The figure below depicts the combination of the subregion-generation software with subregion-sweep software. Navigation between subregions was accomplished by moving to the midpoints of various boundary lines.
References
[1] E. Horváth, C. Pozna, and R. Precup, “Robot Coverage Path Planning Based on Iterative Structured Orientation,” Acta Polytechnica Hungarica, vol. 15, no. 2, 2018.